Círculo Trigonométrico

 O Círculo Trigonométrico, também chamado de Ciclo ou Circunferência Trigonométrica, é uma representação gráfica que auxilia no cálculo das razões trigonométricas.

Círculo trigonométrico e as razões trigonométricas

De acordo com a simetria do círculo trigonométrico temos que o eixo vertical corresponde ao seno e o eixo horizontal ao cosseno. Cada ponto dele está associado aos valores dos ângulos.

Ângulos Notáveis

No círculo trigonométrico podemos representar as razões trigonométricas de um ângulo qualquer da circunferência.

Chamamos de ângulos notáveis aqueles mais conhecidos (30°, 45° e 60°). As razões trigonométricas mais importantes são seno, cosseno e tangente:

Relações Trigonométricas	30°	45°	60°
Seno	1/2	√2/2	√3/2
Cosseno	√3/2	√2/2	1/2
Tangente	√3/3	1	√3

Radianos do Círculo Trigonométrico

A medida de um arco no círculo trigonométrico pode ser dada em grau (°) ou radiano (rad)

• 1° corresponde a 1/360 da circunferência. A circunferência é dividida em 360 partes iguais ligadas ao centro, sendo que cada uma delas apresenta um ângulo que corresponde a 1°.
• 1 radiano corresponde à medida de um arco da circunferência, cujo comprimento é igual ao raio da circunferência do arco que será medido.

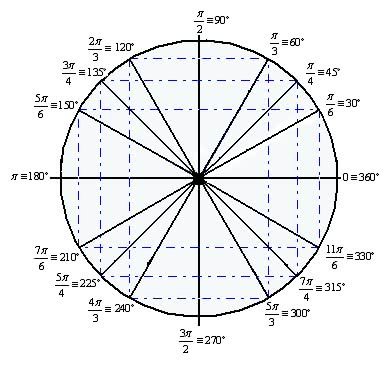Figura do Círculo Trigonométrico dos ângulos expressos em graus e radianos

Para auxiliar nas medidas, confira abaixo algumas relações entre graus e radianos:

• π rad = 180°
• 2π rad = 360°
• π/2 rad = 90°
• π/3 rad = 60°
• π/4 rad = 45°

Obs: Se quiser converter essas unidades de medidas (grau e radiano) utiliza-se a regra de três.

Exemplo: Qual a medida de um ângulo de 30° em radianos?

π rad -180°
x – 30°
x = 30° . π rad/180°
x = π/6 rad

Quadrantes do Círculo Trigonométrico

Quando dividimos o círculo trigonométrico em quatro partes iguais, temos os quatro quadrantes que o constituem. Para compreender melhor, observe a figura abaixo:

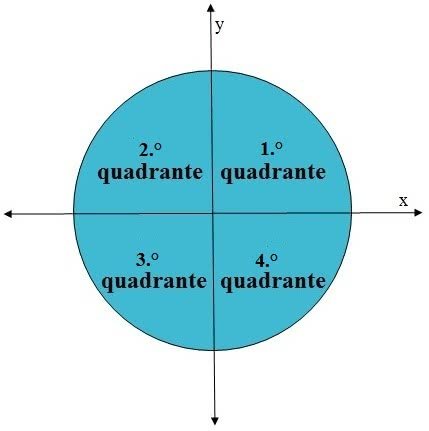
• 1.° Quadrante: 0º
• 2.° Quadrante: 90º
• 3.° Quadrante: 180º
• 4.° Quadrante: 270º

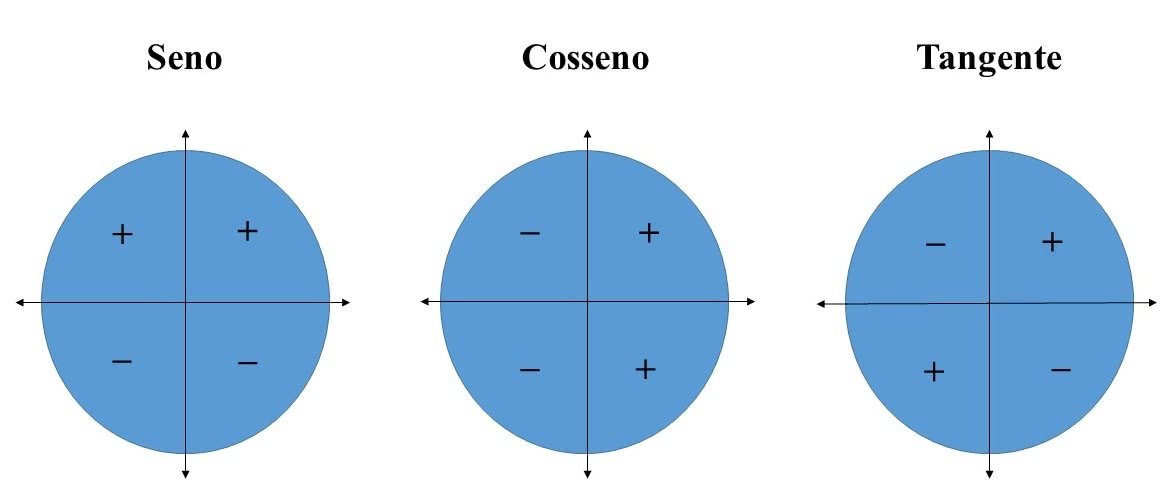
Círculo Trigonométrico e seus Sinais

De acordo com o quadrante em que está inserido, os valores do seno, cosseno e tangente variam.

Ou seja, os ângulos podem apresentar um valor positivo ou negativo.

Para compreender melhor, veja a figura abaixo:

Como Fazer o Círculo Trigonométrico?

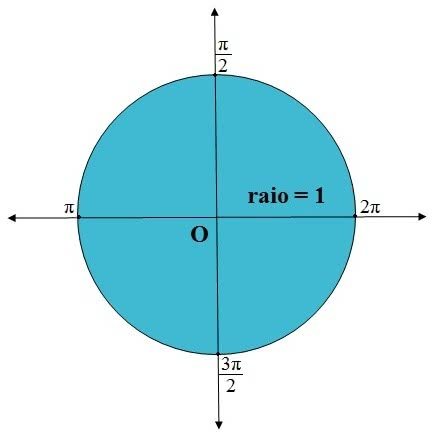
Para fazer um círculo trigonométrico, devemos construí-lo sobre o eixo de coordenadas cartesianas com centro em O. Ele apresenta um raio unitário e os quatro quadrantes.

Razões Trigonométricas

As razões trigonométricas estão associadas às medidas dos ângulos de um triângulo retângulo.

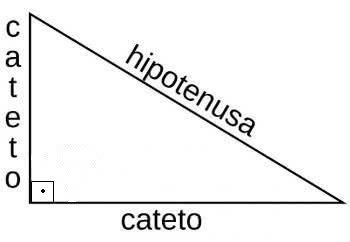
Representação do triângulo retângulo com seus catetos e a hipotenusa

Elas são definidas pelas razões de dois lados de um triângulo retângulo e do ângulo que forma, sendo classificadas em seis maneiras:

Seno (sen)

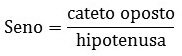
Lê-se cateto oposto sobre a hipotenusa.

Cosseno (cos)

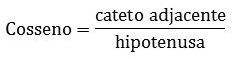
Lê-se cateto adjacente sobre a hipotenusa.

Tangente (tan)

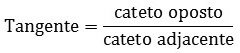
Lê-se cateto oposto sobre cateto adjacente.

Cotangente (cot)

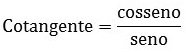
Lê-se cosseno sobre seno.

Cossecante (csc)

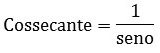
Lê-se um sobre seno.

Secante (sec)

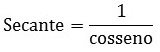
https://www.todamateria.com.br/circulo-trigonometrico/